Question

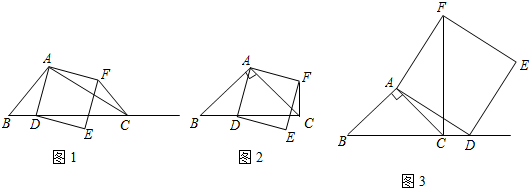
如图，A，F，C，D四点在同一直线上，AF=CD，AB∥DE，且AB=DE．
（1）求证：△ABC≌△DEF；
（2）试判断∠CBF与∠FEC的大小关系，并说明理由．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）求出AC=DF，根据两直线平行，内错角相等可得∠A=∠D，然后利用“边角边”证明即可；
（2）根据全等三角形对应边相等可得EF=BC，全等三角形对应角相等可得∠DFE=∠ACB，然后利用“边角边”证明△FBC和△CEF全等，根据全等三角形对应角相等可得∠CBF=∠FEC．

解答：（1）证明：∵AF=CD，
∴AF+CF=CD+CF，
即AC=DF，
∵AB∥DE，
∴∠A=∠D，
在△ABC和△DEF中，

AC=DF ∠A=∠D AB=DE

，
∴△ABC≌△DEF（SAS）；

（2）解：∠CBF=∠FEC．
理由如下：∵△ABC≌△DEF，
∴EF=BC，∠DFE=∠ACB，
在△FBC和△CEF中，

EF=BC ∠DFE=∠ACB FC=CF

，
∴△FBC≌△CEF（SAS），
∴∠CBF=∠FEC．

点评：本题考查了全等三角形的判定与性质，熟练掌握三角形全等的判定方法并准确识图，找出三角形全等的条件是解题的关键．