题目内容
7.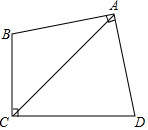 如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,猜想BC,CD,AC间等量关系并证明.
如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,猜想BC,CD,AC间等量关系并证明.
分析 先延长CD至M,使得DM=CB,连接AM,再根据SAS判定△ABC≌△ADM,进而得到AC=AM,∠CAM=90°,判定△CAM是等腰直角三角形,最后根据等腰直角三角形的性质得出结论DM+CD=$\sqrt{2}$AC即可.
解答 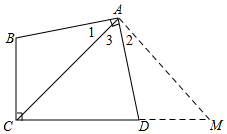 解:BC,CD,AC间等量关系为:BC+DC=$\sqrt{2}$AC.
解:BC,CD,AC间等量关系为:BC+DC=$\sqrt{2}$AC.
理由如下:延长CD至M,使得DM=CB,连接AM,
∵∠BAD=∠BCD=90°,
∴四边形ABCD中,∠B+∠ADC=180°,
又∵∠ADM+∠ADC=180°,
∴∠B=∠ADM,
在△ABC和△ADM中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADM}\\{DM=CB}\end{array}\right.$,
∴△ABC≌△ADM(SAS),
∴AC=AM,∠1=∠2,
又∵∠1+∠3=90°,
∴∠2+∠3=90°,即∠CAM=90°,
∴△CAM是等腰直角三角形,
∴CM=$\sqrt{2}$AC,
即DM+CD=$\sqrt{2}$AC,
∴BC+DC=$\sqrt{2}$AC.
点评 本题主要考查了全等三角形的判定与性质、等腰直角三角形的判定与性质的综合应用,解决问题的关键是作辅助线,构造全等三角形,运用等腰直角三角形和全等三角形的性质进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.某中学九年级学生共450人,其中男生250人,女生200人.该校对九年级所有学生进行了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
(1)请解释“随机抽取了50名男生和40名女生”的合理性;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校九年级学生体育测试成绩不及格的人数.
| 成绩 | 频数 | 百分比 |
| 不及格 | 9 | 10% |
| 及格 | 18 | 20% |
| 良好 | 36 | 40% |
| 优秀 | 27 | 30% |
| 合计 | 90 | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校九年级学生体育测试成绩不及格的人数.
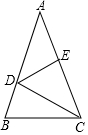 如图,在△ABC中,AB=AC,D在AB上,E在AC上且AE=DE=CD=BC,则∠B=$\frac{540}{7}$度.
如图,在△ABC中,AB=AC,D在AB上,E在AC上且AE=DE=CD=BC,则∠B=$\frac{540}{7}$度.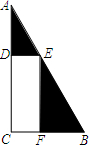 王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.
王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.
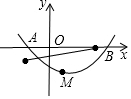 已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.
已知抛物线y=$\frac{1}{6}$(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,M为抛物线的顶点,设动点N(-2,n),求MN+BN的值最小时n的值.