题目内容
【题目】如图，
是
的直径，
是的弦，延长到点
，使
，连结
，过点
作
，垂足为
.
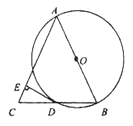
（1）求证：
；
（2）求证：
为的切线；
（3）若的半径为5，
，求的长.
【答案】(1)见解析 ；（2）见解析；(3)DE =
【解析】
（1）根据垂直平分线的判断方法与性质易得AD是BC的垂直平分线，故可得AB=AC；
（2）连接OD，由平行线的性质，易得OD⊥DE，且DE过圆周上一点D故DE为
的切线；
（3）由AB=AC，∠BAC=60°知△ABC是等边三角形，根据等边三角形的性质，可得AB=BC=10，借助三角函数
的定义，求得AD=8, 由勾股定理得BC=6，根据DE=CD·sinC可得答案．
证明：(1)：连接AD
∵AB是⊙O的直径
∴∠ADB=90°
又BD=CD
∴AD是BC的垂直平分线
∴AB=AC
(2)连接OD
∵点O、D分别是AB、BC的中点
∴OD∥AC
又DE⊥AC
∴OD⊥DE
∴DE为⊙O的切线
(3)由AB=AC, 
∵⊙O的半径为5
∴AB=BC=10, AD=8,由勾股定理BC=6
在Rt△CDE中，∠C=∠B
∴DE=CD·sinC=
练习册系列答案
相关题目
【题目】已知二次函数y＝ax2+bx+c（a≠0），函数y与自变量x的部分对应值如下表：
x | …… | ﹣1 | 0 | 1 | 4 | …… |
y | …… | 12 | 6 | 2 | 2 | …… |
（1）求二次函数的解析式；
（2）直接写出不等式ax2+bx+c﹣2＞0的解集是 ．
