题目内容
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
略解:
(1)、△HAB △HGA;
(2)、由△AGC∽△HAB,得AC/HB=GC/AB,即9/y=x/9,故y="81/x" (0<x< )
)
(3)因为:∠GAH= 45°
(1)当∠GAH= 45°是等腰三角形.的底角时,如图(1):可知CG=x= /2
/2
(2)当∠GAH= 45°是等腰三角形.的顶角时, 如图(2):由△HGA∽△HAB
知:HB= AB=9,也可知BG=HC,可得:CG=x=18-

 解析:
解析:
略
(1)、△HAB △HGA;
(2)、由△AGC∽△HAB,得AC/HB=GC/AB,即9/y=x/9,故y="81/x" (0<x<
 )
)(3)因为:∠GAH= 45°
(1)当∠GAH= 45°是等腰三角形.的底角时,如图(1):可知CG=x=
 /2
/2(2)当∠GAH= 45°是等腰三角形.的顶角时, 如图(2):由△HGA∽△HAB
知:HB= AB=9,也可知BG=HC,可得:CG=x=18-


 解析:
解析:略

练习册系列答案
相关题目
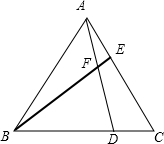 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD. 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD. 13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是
13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是 方作等边△CDE,连接BE.
方作等边△CDE,连接BE. 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的