题目内容
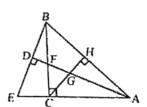
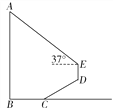
【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() 和
和![]() 相交于点
相交于点![]() .求
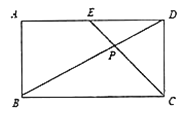
.求![]() 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点![]() 的坐标,从而求得
的坐标,从而求得![]() 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.
【答案】![]()
【解析】
以点B为原点、BC所在的直线为x轴、BA所在的直线为y轴建立直角坐标系,由此可得出点B、A、C、E、D的坐标,利用待定系数法即可得出直线BD、CE的解析式,联立两直线解析式成方程组,解之即可得出点P的坐标,再根据三角形的面积公式即可求出△BPC的面积.
解:如图建立直角坐标系,
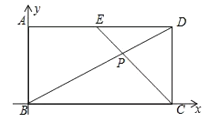
则点B(0,0)、C(4,0)、A(0,2)、D(4,2)、E(2,2).
设直线BD的解析式为y=kx,
将点D(4,2)代入y=kx,得2=4k,
解得:k=![]() ,
,
∴直线BD的解析式为y=![]() x;
x;
设直线CE的解析式为y=mx+n,
将点C(4,0),E(2,2)代入y=mx+n,得![]() ,
,
解得:![]() ,
,
∴直线CE的解析式为y=x+4,
联立直线BD、CE的解析式成方程组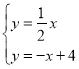 ,
,
解得:![]() ,
,
∴点P的坐标为(![]() ,
,![]() ),
),
∴S△BPC=![]() BCyP=
BCyP=![]() ×4×
×4×![]() =
=![]() .
.

练习册系列答案
相关题目