题目内容
我们把图(1)称作正六边形的基本图,将此基本图不断复制并平移,使得相邻两个基本图的一边重合,这样得到图(2),图(3),…,如此进行下去,直至得图(n).
(1)将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1,4),则x1=
(2)图(n)的对称中心的横坐标为
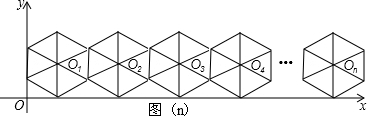
分析:(1)过点O1作O1M⊥y轴于点M,根据正六边形、等腰三角形的性质得出∠BO1M=30°,再由勾股定理求出O1M=2
,即x1=2
;
(2)结合图形分别得出图(2)、图(3)、图(4)的对称中心的横坐标,找到规律,进而得出图(n)的对称中心的横坐标.
| 3 |
| 3 |
(2)结合图形分别得出图(2)、图(3)、图(4)的对称中心的横坐标,找到规律,进而得出图(n)的对称中心的横坐标.
解答:解:
(1)如图,过点O1作O1M⊥y轴于点M,
∵正六边形的中心角=360°÷6=60°,O1C=O1B=O1A=4,
∴∠BO1M=30°,CM=2,
∴O1M=
=
=2
,
∴x1=2
;
(2)由题意,可得图(2)的对称中心的横坐标为
(4
×2)=4
,
图(3)的对称中心的横坐标为
(4
×3)=6
,
图(4)的对称中心的横坐标为
(4
×4)=8
,
…
∴图(n)的对称中心的横坐标为
(4n
)=2n
.

(1)如图,过点O1作O1M⊥y轴于点M,
∵正六边形的中心角=360°÷6=60°,O1C=O1B=O1A=4,
∴∠BO1M=30°,CM=2,
∴O1M=
| O1C2-CM2 |
| 42-22 |
| 3 |
∴x1=2
| 3 |
(2)由题意,可得图(2)的对称中心的横坐标为
| 1 |
| 2 |
| 3 |
| 3 |
图(3)的对称中心的横坐标为
| 1 |
| 2 |
| 3 |
| 3 |
图(4)的对称中心的横坐标为
| 1 |
| 2 |
| 3 |
| 3 |
…
∴图(n)的对称中心的横坐标为
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题借助正六边形考查了规律型:图形的变化类问题,难度适中.关键是通过观察、归纳与总结,得到其中的规律;(2)要注意求的是整个图形的对称中心的横坐标,而不是第n个正六边形的对称中心的横坐标,这也是本题容易出错的地方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 n为正整数)次这样的操作菱形中心O所经过的路径总长为
n为正整数)次这样的操作菱形中心O所经过的路径总长为 如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心.菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过1次这样的操作菱形中心O所经过的路径长为
如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心.菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过1次这样的操作菱形中心O所经过的路径长为

