题目内容
如图，如果AB∥EF，EF∥CD，下列各式正确的是（ ）
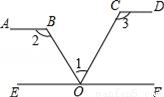
A. ∠1+∠2﹣∠3=90° B. ∠1﹣∠2+∠3=90°
C. ∠1+∠2+∠3=90° D. ∠2+∠3﹣∠1=180°
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
口算心算速算应用题系列答案同步拓展阅读系列答案题目内容
如图，如果AB∥EF，EF∥CD，下列各式正确的是（ ）
A. ∠1+∠2﹣∠3=90° B. ∠1﹣∠2+∠3=90°
C. ∠1+∠2+∠3=90° D. ∠2+∠3﹣∠1=180°
口算心算速算应用题系列答案同步拓展阅读系列答案
B. 
C. 
D. 2m
m
= 2m
=________．
C. －3 D. － 
的解集为_________.