题目内容
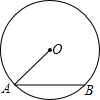 如图,OA是⊙O的半径,AB是弦,∠OAB=45°,OA=8,则AB=________.
如图,OA是⊙O的半径,AB是弦,∠OAB=45°,OA=8,则AB=________.
8
分析:连结OB.则OA=OB,根据∠OAB=45°,可得△OAB是等腰直角三角形,再根据等腰直角三角形的性质即可求解.
解答: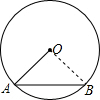 解:连结OB.
解:连结OB.
∵∠OAB=45°,OA=8,
∴∠OBA=45°,OB=8,
∴△OAB是等腰直角三角形,
∴AB=8 .
.
故答案为:8 .
.
点评:考查了圆的认识,等腰直角三角形的性质,本题关键是得到△OAB是等腰直角三角形.

分析:连结OB.则OA=OB,根据∠OAB=45°,可得△OAB是等腰直角三角形,再根据等腰直角三角形的性质即可求解.
解答:
 解:连结OB.
解:连结OB.∵∠OAB=45°,OA=8,
∴∠OBA=45°,OB=8,
∴△OAB是等腰直角三角形,
∴AB=8
 .
.故答案为:8
 .
.点评:考查了圆的认识,等腰直角三角形的性质,本题关键是得到△OAB是等腰直角三角形.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

 上的点E处.
上的点E处. 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
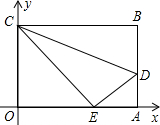
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD= 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.