题目内容
已知tanα=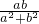 ,其中a、b为常数,且a2+b2≠0,则(a2+b2)sinαcosα-abcos2α的值为________.
,其中a、b为常数,且a2+b2≠0,则(a2+b2)sinαcosα-abcos2α的值为________.
0
分析:先把tanα=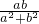 化为a2+b2=
化为a2+b2= =
= 的形式,再代入(a2+b2)sinαcosα-abcos2α进行计算即可.
的形式,再代入(a2+b2)sinαcosα-abcos2α进行计算即可.
解答:∵tanα=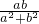 =
= ,
,
∴a2+b2= =
= ,
,
代入原式得,
原式= sinαcosα-abcos2α=abcos2α-abcos2α=0.
sinαcosα-abcos2α=abcos2α-abcos2α=0.
点评:本题考查的是三角函数的商数关系,将a2+b2转化为 是解题的关键.
是解题的关键.
分析:先把tanα=
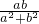 化为a2+b2=
化为a2+b2= =
= 的形式,再代入(a2+b2)sinαcosα-abcos2α进行计算即可.
的形式,再代入(a2+b2)sinαcosα-abcos2α进行计算即可.解答:∵tanα=
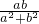 =
= ,
,∴a2+b2=
 =
= ,
,代入原式得,
原式=
 sinαcosα-abcos2α=abcos2α-abcos2α=0.
sinαcosα-abcos2α=abcos2α-abcos2α=0.点评:本题考查的是三角函数的商数关系,将a2+b2转化为
 是解题的关键.
是解题的关键. 
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
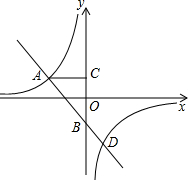 交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO=
交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO= (k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO=
(k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO= ,OB=OC=2.
,OB=OC=2.
 (k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO=
(k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO= ,OB=OC=2.
,OB=OC=2.
 (k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO=
(k≠0)相交于A、D两点.其中D点的纵坐标为-4,直线y=ax+b与y轴相交于B点,作AC⊥y轴于点C,已知tan∠ABO= ,OB=OC=2.
,OB=OC=2.