题目内容
 在△ABC中,D为BC上一点,BD=
在△ABC中,D为BC上一点,BD=| 1 |
| 2 |
| 3 |
分析:过点A作AE⊥BC于点E,根据直角三角形的性质可得出DE,再由勾股定理得出AD,根据三角形的面积,可得出CD,从而得出BD,再根据直角三角形的性质得出∠B的度数.
解答: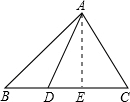 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,
∵∠ADB=120°,
∴∠ADE=60°,
∴∠DAE=30°,
∵AD=2,
∴DE=1,
∴AE=
=
=
,
∵△ADC的面积为3-
,
∴
CD•AE=3-
,
∴CD=2
-2,
∵BD=
DC,
∴BD=
-1,
∴BE=BD+DE=
-1+1=
,
∴AE=BE,
∴∠B=45°.
故答案为45°.
 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,∵∠ADB=120°,
∴∠ADE=60°,
∴∠DAE=30°,
∵AD=2,
∴DE=1,
∴AE=
| AD2-DE2 |
| 22-12 |
| 3 |
∵△ADC的面积为3-
| 3 |
∴
| 1 |
| 2 |
| 3 |
∴CD=2
| 3 |
∵BD=
| 1 |
| 2 |
∴BD=
| 3 |
∴BE=BD+DE=
| 3 |
| 3 |
∴AE=BE,
∴∠B=45°.
故答案为45°.
点评:本题考查了解直角三角形,勾股定理、以及等腰三角形的判定,是基础知识要熟练掌握.

练习册系列答案
相关题目
 已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.
已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积. AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
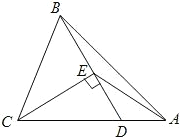
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.