Question

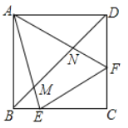
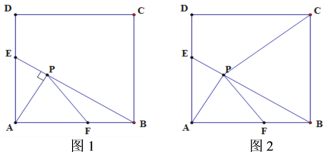
【题目】如图，边长为6的正方形ABCD中，E，F分别是AD，AB上的点，AP⊥BE，P为垂足．

（1）如图1，AF=BF，AE=，点T是射线PF上的一个动点，当△ABT为直角三角形时，求AT的长；

（2）如图2，若AE=AF，连接CP，求证：CP⊥FP．

Answer 1

【答案】（1）当为直角三角形时，的长为3或或；（2）详见解析

【解析】

（1）先根据AE和AB长求出∠ABE=30°，分三种情况：①当点在的上方，，②当点在的下方，，③当时，分别求出AT长即可；

（2）先证∠1=∠3，根据三角函数知识得到，再证，得到∠5=∠6，从而证明CP⊥FP.

解：（1）在正方形中，可得，

在中，，

∴

分三种情况：

①当点在的上方，，

显然此时点和点重合，即；

②当点在的下方，，如图①所示，

在中，由，可得：，

以为圆心长为直径作圆，交射线于点，可知，

∵，是直径，

∴，

∴四边形是矩形，

∴，

在中，

，，

∴；

③当时，如图②所示，

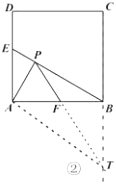
在中，，，，

在中：；

综上所述：当为直角三角形时，的长为3或或；

（2）如图③所示，

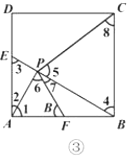
在正方形中，可得，，，

∴，

在中，，易知，，

∴，

∴，

∵，，

在和中可得，

∴，

∵，，

∴，

∵，

∴，

∴，

∵，

∴，即，

∴．