Question

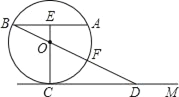
【题目】如图，已知：AB为⊙O的弦（非直径），E为AB的中点，EO的延长线与⊙O相交于C，CM∥AB，BO的延长线与⊙O相交于F，与CM相交于D．

①求证：EC⊥CD；

②当EO：OC=1：3，CD=4时，求⊙O的半径．

Answer 1

【答案】①证明见解析②

【解析】

①根据垂径定理不难得出OE⊥AB．又有AB∥CM，由此便可证得；
②AB∥CD，不难得出EO：OC=1：3；然后用半径分别表示出OC，OD，CD，根据勾股定理来求出半径的值．

①证明：E为弦AB（非直径）的中点，O为圆心，

∴∠OEB=90°，

∵∠ECD=∠OEB=90°，

即EC⊥CD；

②解：∵CD∥AB，EO：OC=1：3，

∴，

设OC=BO=x，则OD=3x，又CD=4，

在Rt△OCD中，由OC2+CD2=OD2，x2+42=（3x）2，

解得：x1= ，x2=﹣（舍去），

∴BO=，

即⊙O的半径为．