题目内容
 如图,反比例函数
如图,反比例函数 (k≠0)的图象经过点(-3,1),并与直线
(k≠0)的图象经过点(-3,1),并与直线 交于A(x1,y1)、B(x2,y2)两点,并且x1、x2满足
交于A(x1,y1)、B(x2,y2)两点,并且x1、x2满足 .
.
(1)求反比例函数的解析式;
(2)求m的值及△AOB的面积.
解:(1)把(-3,1)代入到 ,
,
得:k=-3×1=-3,
∴反比例函数的解析式为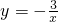 ;
;
(2)∵反比例函数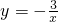 与直线
与直线 交于A(x1,y1)、B(x2,y2)两点,
交于A(x1,y1)、B(x2,y2)两点,
∴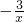 =
= ,
,
整理得:- ,
,
∴x1+x2=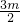 ,x1•x2=
,x1•x2=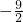 ,
,
∵ ,
,
整理得: =
= ,
,
即: =
= ,
,
解得m=1,
∴直线的解析式为y= x+1,
x+1,
∴A(3,-1)、B( ,2),
,2),
∴直线AB与y轴交于(0,1),
∴S△AOB= ×1×(3+
×1×(3+ )=
)= .
.
分析:(1)将点(-3,1)代入反比例函数的解析式 即可得到反比例函数的解析式;
即可得到反比例函数的解析式;
(2)联立得到关于x的一元二次方程并利用 解得m的值及△AOB的面积.
解得m的值及△AOB的面积.
点评:本题考查了反比例函数的综合知识,特别是与“根与系数的关系”的结合更是一个难点.
 ,
,得:k=-3×1=-3,
∴反比例函数的解析式为
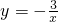 ;
;(2)∵反比例函数
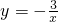 与直线
与直线 交于A(x1,y1)、B(x2,y2)两点,
交于A(x1,y1)、B(x2,y2)两点,∴
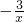 =
= ,
,整理得:-
 ,
,∴x1+x2=
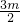 ,x1•x2=
,x1•x2=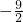 ,
,∵
 ,
,整理得:
 =
= ,
,即:
 =
= ,
,解得m=1,
∴直线的解析式为y=
 x+1,
x+1,∴A(3,-1)、B(
 ,2),
,2),∴直线AB与y轴交于(0,1),
∴S△AOB=
 ×1×(3+
×1×(3+ )=
)= .
.分析:(1)将点(-3,1)代入反比例函数的解析式
 即可得到反比例函数的解析式;
即可得到反比例函数的解析式;(2)联立得到关于x的一元二次方程并利用
 解得m的值及△AOB的面积.
解得m的值及△AOB的面积.点评:本题考查了反比例函数的综合知识,特别是与“根与系数的关系”的结合更是一个难点.

练习册系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数