题目内容
【题目】小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整.例题:求一元二次方程![]() 的两个解.
的两个解.
(1)解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解.解方程:![]() ;
;
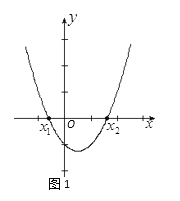
(2)解法二:利用二次函数图象与坐标轴的交点求解,如图1所示,把方程![]() 的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
的解看成是二次函数y= 的图象与x轴交点的横坐标,即x1,x2就是方程的解.
(3)解法三:利用两个函数图象的交点求解.
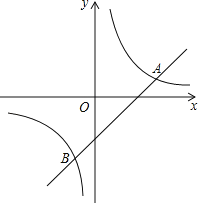
①把方程![]() 的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;
②画出这两个函数的图象,用x1,x2在x轴上标出方程的解.
【答案】(1)过程见解析,![]() =
=![]() ,
,![]() =
=![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ,
,![]() ;②见解析
;②见解析
【解析】
(1)利用公式法求解即可.
(2)因为![]() 表示的是函数
表示的是函数![]() 与
与![]() 轴交点时的情境,即函数
轴交点时的情境,即函数![]() 的值为0时,所以把方程
的值为0时,所以把方程![]() 的解看成是二次函数
的解看成是二次函数![]() 的图象与轴
的图象与轴![]() 交点的横坐标,可以得到答案.
交点的横坐标,可以得到答案.
(3)①由![]() 变形为
变形为![]() ,因为
,因为![]() 都是变量
都是变量![]() 的函数,所以
的函数,所以![]() ,当两个函数的函数值相等,即此时的函数值为两个函数的交点的纵坐标,从而观察图像可以得到交点的横坐标得到答案.
,当两个函数的函数值相等,即此时的函数值为两个函数的交点的纵坐标,从而观察图像可以得到交点的横坐标得到答案.
②利用一次函数与二次函数的作图方法在同一直角坐标系中作出图像即可.
解:(1)解:∵![]() ,
,
∴![]() .∴
.∴![]() .
.
∴原方程的解是![]() =
=![]() ,
,![]() =
=![]() .
.
(2)因为求二次函数.![]() 与
与![]() 轴交点时,把交点的纵坐标
轴交点时,把交点的纵坐标![]() 代入函数解析式得到
代入函数解析式得到![]() 的解是交点的横坐标,所以求方程
的解是交点的横坐标,所以求方程![]() 的解时就可以画出
的解时就可以画出![]() 的图像,观察交点的横坐标就是方程
的图像,观察交点的横坐标就是方程![]() 的解.
的解.
故答案为![]() .
.
(3)因为![]() ,
,
所以![]() ,因为
,因为![]() 都是变量
都是变量![]() 的函数,
的函数,
建立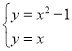
考查的两个函数分别是![]() ,两个函数的交点的横坐标就是方程
,两个函数的交点的横坐标就是方程![]() 的解.
的解.
故答案为:![]() 与
与![]() ..
..
每画出正确函数图象如下:
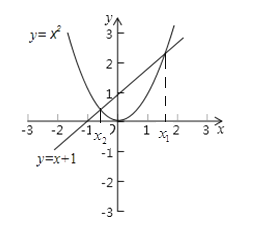

【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.