题目内容
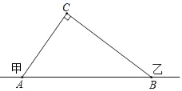
【题目】直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点.
(k为常数)相交于A、B两点.
(1)若点A的横坐标为3,点B的纵坐标为﹣4
①直接写出:k=____,m=____;
②点C在第一象限内是双曲线y=![]() 的点,当S△OAC=9时,求点C的坐标;
的点,当S△OAC=9时,求点C的坐标;
(2)将直线y=mx向右平移得到直线y=mx+b,交双曲线y=![]() 于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
于点E(4,y1)和F(﹣2,y2),直接写出不等式mx2+bx<k的解集:_____.
【答案】(1)①12,![]() ;②点C的坐标为(6,2)或(
;②点C的坐标为(6,2)或(![]() ,8);(2)﹣2<x<4.
,8);(2)﹣2<x<4.
【解析】
(1)①根据正比例函数与双曲线的交点关于原点对称得出A(3,4),B(-3,-4),进而得出k=3×4=12,m=![]() ;
;
②如图,过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,设C(x,![]() ),x>0.利用反比例函数比例系数k的几何意义得出S△ONC=S△OAM,再推出S△OAC=S梯形AMNC=9,根据梯形的面积公式列式计算即可;
),x>0.利用反比例函数比例系数k的几何意义得出S△ONC=S△OAM,再推出S△OAC=S梯形AMNC=9,根据梯形的面积公式列式计算即可;
(2)由双曲线y=![]() 过点E(4,y1)和F(-2,y2),得出E(4,
过点E(4,y1)和F(-2,y2),得出E(4,![]() ),F(-2,-
),F(-2,-![]() ),将E、F两点的坐标代入y=mx+b,得到
),将E、F两点的坐标代入y=mx+b,得到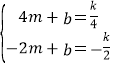 ,解得
,解得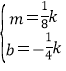 ,进而解不等式mx2+bx<k即可.
,进而解不等式mx2+bx<k即可.
(1) ①∵直线y=mx(m为常数)与双曲线y=![]() (k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为-4,
(k为常数)相交于A、B两点,点A的横坐标为3,点B的纵坐标为-4,
∴A(3,4),B(-3,-4),
∴k=3×4=12,m=![]() ;
;
②如图,过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,设C(x,![]() ),x>0.
),x>0.
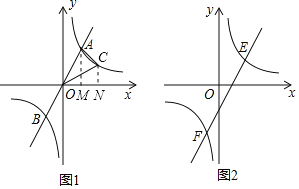
∵S△OAC+S△ONC=S梯形AMNC+S△OAM,S△ONC=S△OAM,
∴S△OAC=S梯形AMNC=9,
∴S梯形AMNC=![]() (AM+CN)MN=
(AM+CN)MN=![]() (4+
(4+![]() )|x﹣3|=9,
)|x﹣3|=9,
当x>3时,化简整理方程,得2x2﹣9x﹣18=0,解得x1=6,x2=﹣![]() (舍去),此时C
(舍去),此时C
(6,2);
当x<3时,化简整理方程,得2x2+9x﹣18=0,解得x1=﹣6(舍去),x2=![]() ,此时C(
,此时C(![]() ,8);
,8);
综上所述,所求点C的坐标为(6,2)或(![]() ,8);
,8);
(2) 将直线y=mx向右平移得到直线y=mx+b.
∵双曲线y=![]() 过点E(4,y1)和F(-2,y2),
过点E(4,y1)和F(-2,y2),
∴E(4,![]() ),F(-2,-
),F(-2,-![]() ),
),
∵直线y=mx+b过点E、F,
∴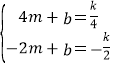 ,解得
,解得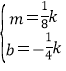 ,
,
∴不等式mx2+bx<k即为![]() kx2-
kx2-![]() kx<k,
kx<k,
∵k≠0,
∴x2-2x<8,
∴x2-2x-8<0,
∴-2<x<4.
故答案为:﹣2<x<4.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案