题目内容
 如图,在△ABC中,过BC边上的中点D作垂线交边AB于点E,若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12.
如图,在△ABC中,过BC边上的中点D作垂线交边AB于点E,若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12.(1)图中与线段EC相等的线段是
(2)则线段DE的长为
考点:线段垂直平分线的性质
专题:
分析:(1)根据“垂直平分线上任意一点,到线段两端点的距离相等”填空;
(2)运用线段垂直平分线定理可得BE=CE,再根据已知条件“△EDC的周长为24,△ABC与四边形AEDC的周长之差为12”表示出线段之间的数量关系,联立关系式后求解.
(2)运用线段垂直平分线定理可得BE=CE,再根据已知条件“△EDC的周长为24,△ABC与四边形AEDC的周长之差为12”表示出线段之间的数量关系,联立关系式后求解.
解答:解:(1)如图,∵ED是BC的中垂线,
∴BE=EC.
故答案是:BE;
(2)∵DE是BC边上的垂直平分线,
∴BE=CE.
∵△EDC的周长为24,
∴ED+DC+EC=24,①
∵△ABC与四边形AEDC的周长之差为12,
∴(AB+AC+BC)-(AE+ED+DC+AC)=(AB+AC+BC)-(AE+DC+AC)-DE=12,
∴BE+BD-DE=12,②
∵BE=CE,BD=DC,
∴①-②得,DE=6.
故答案是:6.
∴BE=EC.
故答案是:BE;
(2)∵DE是BC边上的垂直平分线,
∴BE=CE.
∵△EDC的周长为24,
∴ED+DC+EC=24,①
∵△ABC与四边形AEDC的周长之差为12,
∴(AB+AC+BC)-(AE+ED+DC+AC)=(AB+AC+BC)-(AE+DC+AC)-DE=12,
∴BE+BD-DE=12,②
∵BE=CE,BD=DC,
∴①-②得,DE=6.
故答案是:6.
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
相关题目
下列各组数中,能构成直角三角形的三边的长度是( )
| A、3,5,7 | ||||||
B、
| ||||||
| C、0.3,0.5,0.4 | ||||||
| D、5,22,23 |
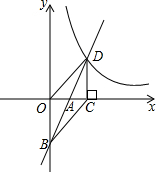 如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=
如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=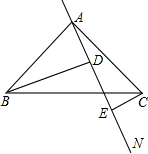 如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由.
如图,已知在Rt△ABC中,AB=AC,∠BAC=90°,AN是过点A的任意一直线,BD⊥AN于点D,CE⊥AN于点E,则BD,CE,DE之间存在着怎样的关系?请说明理由. 如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是
如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是