题目内容
解下列不等式组,并把解集在数轴上表示出来.
(1)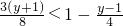 ;
;
(2) .
.
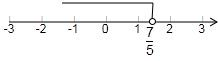
解:(1)原不等式可化为3(y+1)<8-2(y-1),
解得,y< ,
,
在数轴上表示为:
(2)由①得,x≤- ,
,
由②得,x< ,
,
故此不等式组的解集为: ,
,
在数轴上表示为:
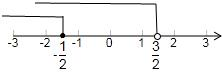
分析:(1)先把不等式中的分母去掉,再根据不等式的基本性质求出y的取值范围,在数轴上表示出来即可;
(2)先分别求出各不等式的解集,再求出其公共解集即可.
点评:本题考查的是不等式的基本性质:
基本性质1:不等式两边同时加上或减去同一个整式,不等号的方向不变;
基本性质2:不等式两边同时乘以或除以同一个正数,不等号的方向不变;
基本性质3:不等式两边同时乘以或除以同一个负数,不等号的方向改变.
解得,y<
 ,
,在数轴上表示为:

(2)由①得,x≤-
 ,
,由②得,x<
 ,
,故此不等式组的解集为:
 ,
,在数轴上表示为:
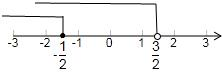
分析:(1)先把不等式中的分母去掉,再根据不等式的基本性质求出y的取值范围,在数轴上表示出来即可;
(2)先分别求出各不等式的解集,再求出其公共解集即可.
点评:本题考查的是不等式的基本性质:
基本性质1:不等式两边同时加上或减去同一个整式,不等号的方向不变;
基本性质2:不等式两边同时乘以或除以同一个正数,不等号的方向不变;
基本性质3:不等式两边同时乘以或除以同一个负数,不等号的方向改变.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目