题目内容
18. 已知△ABC的外接圆0的半径为8,AB=6,则sinC=$\frac{3}{8}$.
已知△ABC的外接圆0的半径为8,AB=6,则sinC=$\frac{3}{8}$.
分析 如图,作辅助线;首先证明∠C=∠D,∠ABD=90°,得到sin∠C=sin∠D,借助三角函数的定义即可解决问题.
解答  解:如图,作⊙O的直径AD,连接BD;
解:如图,作⊙O的直径AD,连接BD;
则∠C=∠D,∠ABD=90°,AD=2×8=16,
∴sin∠C=sin∠D=$\frac{AB}{AD}=\frac{6}{16}=\frac{3}{8}$,
故答案为$\frac{3}{8}$.
点评 该题主要考查了圆周角定理、三角函数的定义等知识点及其应用问题;解题的关键是作辅助线,灵活运用圆周角定理、三角函数的定义等知识点来分析、判断、解答.

练习册系列答案
相关题目
8.下列命题中,正确的是( )
| A. | 有理数和数轴上的点一一对应 | |
| B. | 等腰三角形的对称轴是它的顶角平分线 | |
| C. | 全等的两个图形一定成轴对称 | |
| D. | 有理数和无理数统称为实数 |
10.下列数:-3,1,-2,0中,最大的是( )
| A. | -3 | B. | 0 | C. | -2 | D. | 1 |
7.某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
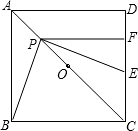 长为4的正方形ABCD中,P是对角线AC上一动点,过点P作PF⊥CD于点F,作PE⊥PB交射线CD于点E.
长为4的正方形ABCD中,P是对角线AC上一动点,过点P作PF⊥CD于点F,作PE⊥PB交射线CD于点E.