题目内容
随着多边形边数的增加，每增加一条边，则
- A.外角和增加180°
- B.对角线增加1条
- C.内角和增加180°
- D.内角和增加360°
C
分析：利用多边形的内角和定理和外角和特征即可解决问题．
解答：∵n边形的内角和是（n-2）•180°，
当边数增加一条就变成n+1，则内角和是（n-1）•180度，
内角和增加：（n-1）•180°-（n-2）•180°=180°；
根据多边形的外角和特征，边数变化外角和不变．
故选C．
点评：本题主要考查了多边形的内角和定理与外角和特征．先设这是一个n边形是解题的关键．
分析：利用多边形的内角和定理和外角和特征即可解决问题．
解答：∵n边形的内角和是（n-2）•180°，
当边数增加一条就变成n+1，则内角和是（n-1）•180度，
内角和增加：（n-1）•180°-（n-2）•180°=180°；
根据多边形的外角和特征，边数变化外角和不变．
故选C．
点评：本题主要考查了多边形的内角和定理与外角和特征．先设这是一个n边形是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
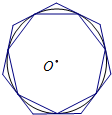（2013•北仑区二模）割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．试用这个方法解决问题：如图，⊙的内接多边形周长为3，⊙O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（ ）