题目内容
16.先化简,再求值:2(x+1)2-3(x-3)(3+x)+(x+5)(x-2),其中x满足x2+y2=2x-4y-5.分析 利用配方法把原式化为平方和的形式,根据非负数的性质求出x、y的值,根据乘法公式把原式化简,代入计算即可.
解答 解:∵x满足x2+y2=2x-4y-5,
∴x2-2x+1+y2+4y+4=0,
(x-1)2+(y+2)2=0,
则x-1=0,y+2=0,
解得,x=1,y=-2,
原式=2(x2+2x+1)-3(x2-9)+x2+3x-10
=2x2+4x+2-3x2+27+x2+3x-10
=7x+19
当x=1时,原式=26.
点评 本题考查的是整式的混合运算、非负数的性质和配方法的应用,掌握整式的乘法公式、正确运用配方法是解题的关键.

练习册系列答案
相关题目
6.(-2a3)2等于( )
| A. | 4a5 | B. | 4a6 | C. | 4a9 | D. | -4a6 |
7.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | 2+$\sqrt{3}$=2$\sqrt{3}$ | C. | 2x-2=$\frac{1}{2{x}^{2}}$ | D. | (-a3)2=a6 |
8. 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )| A. | 上,下 | B. | 右,后 | C. | 左,右 | D. | 左,后 |
5.下列计算正确的是( )
| A. | (a3)2=a5 | B. | a3+a2=a5 | C. | a5÷a2=a3 | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
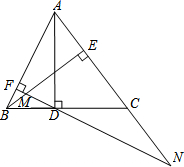 如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N.
如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交BE于M,FD、AC的延长线交于点N. 如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=-$\frac{3}{4}$x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=-$\frac{3}{4}$x+b与圆相切于点M,分别交x轴、y轴于B、C两点.