题目内容
直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为点E,F.

1.(1)求证:△FOE≌ △DOC;
2.(2)求sin∠OEF的值;
3. (3)若直线EF与线段AD,BC分别相交于点G,H,求![]() 的值.
的值.
1.(1)证明:∵E,F分别为线段OA,OB的中点,
∴EF∥AB,AB=2EF,
∵AB=2CD,
∴EF=CD,
∵AB∥CD,
∴EF∥CD,
∴∠OEF=∠OCD,∠OFE=∠ODC,
∴△FOE≌ △DOC;
2.(2)在△ABC中,∵∠ABC=90°,
∴![]()
![]() .
.
∵EF∥AB,
∴∠OEF=∠CAB,
∴![]()
3.(3)∵△FOE≌ △DOC,
∴OE=OC,
∵AE=OE,AE=OE=OC,
∴![]() .
.
∵EF∥AB,
∴△CEH∽△CAB,
∴![]() ,
,
∴![]() , …………………8分
, …………………8分
∵EF=CD,
∴![]() ,
,![]() ,
,
同理![]() ,∴
,∴![]() ,
,
∴
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
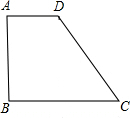 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为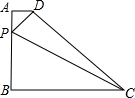 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为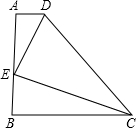 下结论:
下结论: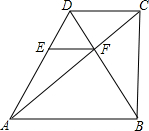 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.