��Ŀ����
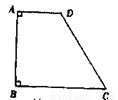
��֪����ͼ���ı���ABCD�У���A=��B=90�㣬��C=60�㣬CD=2AD,AB=4.
��1����AB����������P,ʹPC+PD��С��
��2�������1����PC+PD����Сֵ.
��ϰ��ϵ�д�
 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
�����Ŀ
��Ŀ����
��֪����ͼ���ı���ABCD�У���A=��B=90�㣬��C=60�㣬CD=2AD,AB=4.
��1����AB����������P,ʹPC+PD��С��
��2�������1����PC+PD����Сֵ.

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�