题目内容
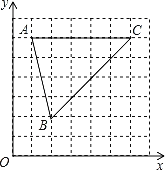
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() 三个点.
三个点.
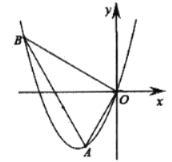
(1)求抛物线解析式;
(2)若点![]() ,
,![]() 为该抛物线上的两点,且
为该抛物线上的两点,且![]() .求
.求![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使点
重合),使点![]() ,点
,点![]() 到直线
到直线![]() 的距离之和最大?若存在,求
的距离之和最大?若存在,求![]() 的度数,并直接写出点
的度数,并直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,60°,
;(3)存在,60°,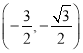
【解析】
(1)利用待定系数法将O,A,B三个点的坐标代入y=ax2+bx+c即可求得a,b,c的值,进而求得抛物线解析式.
(2)设出点P关于对称轴对称的点的坐标,利用数形结合的思想求解即可.
(3)分析如图,运用点到直线的距离的性质求解即可.
解:(1)![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,
,
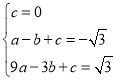 ,解得
,解得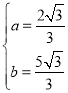 .
.
![]()
(2)由(1)抛物线开口向上,对称轴为直线![]() ,得
,得
点![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() .
.
当![]() 时,
时,![]() 随
随![]() 的增大而小.
的增大而小.
当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
![]() 当
当![]() 时,
时,![]() .
.
(3)存在.
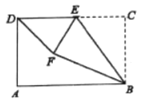
如图,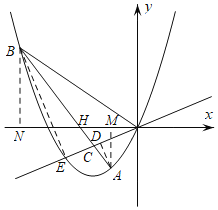
分别过点A,B作AM⊥x轴于点M,BN⊥x轴于点N,并作BE⊥OC于点E,AD⊥OC于点D.
∵AD≤AC,BE≤BC,
∴AD+BE≤AC+BC=AB.
∴当OC⊥AB时,点A,点B到直线OC的距离之和最大.
过点A作AM⊥x轴于点M,过B作BN⊥x轴于点N.AB与x轴交于H.
又∵A(-1,-![]() ),B(-3,
),B(-3,![]() ),
),
∴AM=BN=![]() ,∠AMH=∠BNH=90°.
,∠AMH=∠BNH=90°.
又∵∠AHO=∠BHN,
∴△AMH≌△BNH.
∴MH=NH.
又∵OM=1,ON=3,
∴OM=MH=NH=1.
![]() ,
,
![]() .
.
同理:![]() .
.
![]()
点![]() 坐标为
坐标为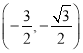 .
.

【题目】已知函数![]() ,其中
,其中![]() 与
与![]() 成反比例
成反比例![]() 与
与![]() 成正比例,函数的自变量
成正比例,函数的自变量![]() 的取值范围是
的取值范围是![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() 的值均为
的值均为![]() 。
。
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探宄:①根据解析式,选取适当的自变量![]() ,并完成下表:
,并完成下表:
|
| ... | ||||||||
| ... |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.
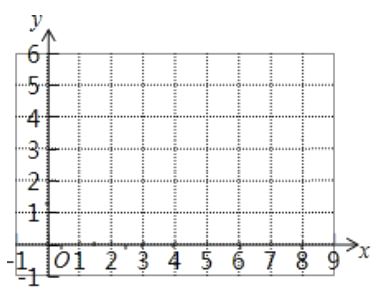
(3)结合画出的函数图象,解决问题:
①当![]() ,
,![]() ,
,![]() 时,函数值分别为
时,函数值分别为![]() ,则
,则![]() 的大小关系为: (用“
的大小关系为: (用“![]() ”或“
”或“![]() ”表示)
”表示)
②若直线![]() 与该函数图象有两个交点,则
与该函数图象有两个交点,则![]() 的取值范围是 ,此时,
的取值范围是 ,此时,![]() 的取值范围是 .
的取值范围是 .