题目内容
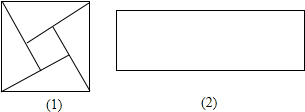
如图,将一宽为2cm的纸条,沿BC折叠,使∠CAB=45°,则折叠后重合部分的面积为( )
A.

B.

C.

D.

【答案】分析:作出AB边上的高,求出AC的长;根据翻折不变性及平行线的性质,求出AC=AB,再利用三角形的面积公式解答即可.
解答: 解:作CD⊥AB,
解:作CD⊥AB,
∵CE∥AB,
∴∠1=∠2,
根据翻折不变性,∠1=∠BCA,
故∠2=∠BCA.
∴AB=AC.
又∵∠CAB=45°,
∴在Rt△ADC中,
AC= =
= =2
=2 ,
,
AB=2 .
.
则S△ABC= AB•CD=
AB•CD= ×2
×2 ×2=2
×2=2 .
.
故选A.
点评:此题考查了翻折变换,解题过程中利用翻折不变性是解题的关键.还要注意翻折过程中的特殊图形,以便利用其性质.
解答:
 解:作CD⊥AB,
解:作CD⊥AB,∵CE∥AB,
∴∠1=∠2,
根据翻折不变性,∠1=∠BCA,
故∠2=∠BCA.
∴AB=AC.
又∵∠CAB=45°,
∴在Rt△ADC中,
AC=
 =
= =2
=2 ,
,AB=2
 .
.则S△ABC=
 AB•CD=
AB•CD= ×2
×2 ×2=2
×2=2 .
.故选A.
点评:此题考查了翻折变换,解题过程中利用翻折不变性是解题的关键.还要注意翻折过程中的特殊图形,以便利用其性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,将一宽为2cm的纸条,沿BC折叠,使∠CAB=45°,则折叠后重合部分的面积为( )
如图,将一宽为2cm的纸条,沿BC折叠,使∠CAB=45°,则折叠后重合部分的面积为( )A、2
| ||
B、
| ||
C、3
| ||
D、4
|