题目内容
如图，AB是直径为10cm的⊙O的一条弦，若AB=
cm，则△OAB的面积是
- A.
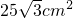
- B.
- C.
- D.
C
分析：过圆心O作OD⊥AB于点D．由垂径定理求得AD=BD=
AB；然后在直角三角形OAD中利用勾股定理即可求得OD的长度；最后根据三角形的面积公式来求△OAB的面积．
解答：
解：过圆心O作OD⊥AB于点D，则AD=BD=AB=
．
在Rt△OAD中，OA=5cm，AD=，
由勾股定理知，OD=
=
，
则△OAB的面积为：AB•OD=×5
cm×cm=．
故选C．
点评：本题考查了垂径定理、勾股定理．此类在圆中涉及弦长、半径的计算的问题，常把半弦长，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．
分析：过圆心O作OD⊥AB于点D．由垂径定理求得AD=BD=
AB；然后在直角三角形OAD中利用勾股定理即可求得OD的长度；最后根据三角形的面积公式来求△OAB的面积．解答：
解：过圆心O作OD⊥AB于点D，则AD=BD=AB=．在Rt△OAD中，OA=5cm，AD=
，由勾股定理知，OD=
=，则△OAB的面积为：
AB•OD=×5cm×cm=．故选C．
点评：本题考查了垂径定理、勾股定理．此类在圆中涉及弦长、半径的计算的问题，常把半弦长，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．
练习册系列答案
阅读快车系列答案
相关题目
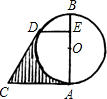已知如图，AB是⊙O直径，∠C的两边分别与⊙O相切于A、D两点．DE⊥AB，垂足为E，AE=3，BE=1，则图中阴影部分面积（ ）A、4
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
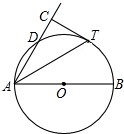如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
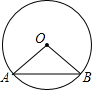（2008•宝安区二模）如图，AB是直径为10cm的⊙O的一条弦，若AB=
cm，则△OAB的面积是（ ）
