题目内容
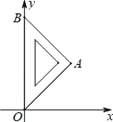
【题目】如图，O为坐标原点，△OAB是等腰直角三角形，∠OAB=90°，点B的坐标为(0，2
)，将该三角形沿x轴向右平移得到Rt△O′A′B′，此时点B′的坐标为(2，2)，则线段OA在平移过程中扫过部分的图形面积为( )
A. 2B. 
C. 4D. 
【答案】C
【解析】
利用平移的性质得出AA′的长，根据等腰直角三角形的性质得到AA′对应的高，再结合平行四边形面积公式求出即可．
解：∵点B的坐标为（0，2
），将该三角形沿x轴向右平移得到Rt△O′A′B′，此时点B′的坐标为（2，2），
∴AA′=BB′=2，
∵△OAB是等腰直角三角形，
∴A（，），
∴AA′对应的高为，
∴线段OA在平移过程中扫过部分的图形面积为2×=4．
故答案为：4．
练习册系列答案
相关题目
