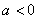题目内容
如图1,在平面直角坐标系中, 为坐标原点.直线
为坐标原点.直线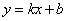 与抛物线
与抛物线 同时经过
同时经过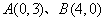 .
.
(1)求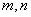 的值.
的值.
(2)点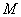 是二次函数图象上一点,(点
是二次函数图象上一点,(点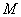 在
在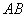 下方),过
下方),过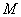 作
作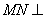
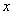 轴,与
轴,与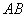 交于点
交于点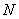 ,与
,与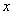 轴交于点
轴交于点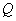 .求
.求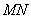 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点N,使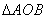 和
和 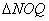 相似?如果存在,请求点N的坐标;如果不存在,请说明理由.
相似?如果存在,请求点N的坐标;如果不存在,请说明理由.

解:
(1) 抛物线
抛物线 经过两点
经过两点

 解得
解得
所以二次函数的表达式为 . …………………………….2分
. …………………………….2分
(2)可求经过AB两点的一次函数的解析式为 .
.



 当
当 时,
时,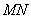 取得最大值为4.……………………………….4分
取得最大值为4.……………………………….4分
(3)存在.
①当 时,(如图1)
时,(如图1)
可证: ,
,

 ∽
∽ .
.








 ,
,



 .
. ------------------------6分
------------------------6分
②当N为AB中点时,(如图2)
 ,
,

 ∽
∽ .此时
.此时 .----------------------7分
.----------------------7分
 满足条件的N
满足条件的N 或N
或N ------------------------------------------------------8分
------------------------------------------------------8分

练习册系列答案
相关题目

 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象交于C、D两点,则AD和BC有怎样的数量关系?
的图象交于C、D两点,则AD和BC有怎样的数量关系? 进行研究(如图①),此时我发现AD=BC.
进行研究(如图①),此时我发现AD=BC. ,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.


 总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗? .
. 的图象与x轴只有一个公共点,求实数a的值.
的图象与x轴只有一个公共点,求实数a的值.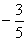 <
<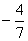 B.
B.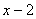 是有理数,它的倒数是
是有理数,它的倒数是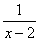
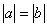 ,则
,则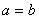 D.若
D.若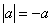 ,则
,则