题目内容
如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM。

证明:(1)在正方形ABCD中,AB=BC,∠ABC=90°,
在△ABE和△CBF中,
AB=BC ∠ABC=∠ABC BE=BF ,
∴△ABE≌△CBF(SAS),
∴∠BFC=∠BEA;
(2)连接DG,在△ABG和△ADG中,
AB=AD ∠DAC=∠BAC=45° AG=AG ,
∴△ABG≌△ADG(SAS),
∴BG=DG,∠2=∠3,
∵BG⊥AE,
∴∠BAE+∠2=90°,
∵∠BAD=∠BAE+∠4=90°,
∴∠2=∠3=∠4,
 ∵GM⊥CF,
∵GM⊥CF,
∴∠BCF+∠1=90°,
又∠BCF+∠BFC=90°,
∴∠1=∠BFC=∠2,
∴∠1=∠3,
在△ADG中,∠DGC=∠3 +45°,
+45°,
∴∠DGC也是△CGH的外角,
∴D、G、M三点共线,
∵∠3=∠4(已证),
∴A M=DM,
M=DM,
∵DM=DG+GM=BG+GM,
∴AM=BG+GM.

练习册系列答案
相关题目


 ;④3≤n≤4中,
;④3≤n≤4中,

 B.
B. C.
C. D.
D.
 线y=2x+4与
线y=2x+4与 轴、
轴、 轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线
轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线 上,将正方形ABCD沿
上,将正方形ABCD沿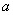 个单位长度后,点C恰好落在此双曲线上,则
个单位长度后,点C恰好落在此双曲线上,则

 (B)
(B) (C)2 (D)-2
(C)2 (D)-2 -20120=
-20120=