Question

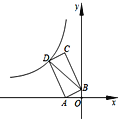
【题目】以四边形的边为斜边分别向外侧作等腰直角三角形，直角顶点分别为顺次连接这四个点，得四边形．

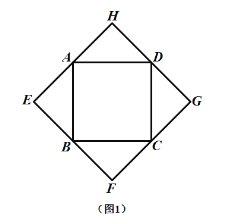
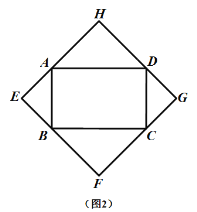
（1）如（图1）．当四边形为正方形时，我们发现四边形是正方形；如（图2），当四边形为矩形时，请判断：四边形的形状(不要求证明)；

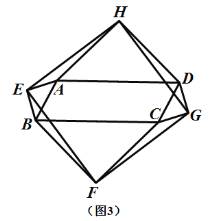
（2）如（图3），当四边形为一般平行四边形时 ，设

①试用含的代数式表示；

②求证：四边形是正方形，

Answer 1

【答案】（1）四边形的形状是正方形；（2）①；②见解析

【解析】

（1）根据△AHD和△DGC是等腰直角三角形，得出∠EHG＝90°，从而判定四边形EFGH是矩形，再判断出△AEB≌△DGC，得出HE＝HG，即可推出结论，

（2）①根据平行四边形的性质得出，∠BAD＝180°﹣α，根据△HAD和△EAB是等腰直角三角形，得到∠HAD＝∠EAB＝45°，求出∠HAE即可；

②根据△AEB和△DGC是等腰直角三角形，得出AE＝AB，DG＝CD，平行四边形的性质得出AB＝CD，求出∠HDG＝90°+∠ADC＝∠HAE，根据SAS证△HAE≌△HDG，根据全等三角形的性质即可得出HE＝HG；证明过程类似求出GH＝GF，FG＝FE，推出GH＝GF＝EF＝HE，得出菱形EFGH，证△HAE≌△HDG，求出∠AHD＝90°，∠EHG＝90°，即可推出结论．

解: 证明：（1）四边形EFGH是正方形；

理由：∵△AHD是等腰直角三角形，

∴∠HDA＝∠HAD＝45°，

∴∠EHG＝90°，

同理：∠HEF＝∠EFG＝90°，

∴四边形EFGH是矩形，

∵△AHD是等腰直角三角形，

∴HA＝HD，

在矩形ABCD中，AB＝CD，

在△AEB和△DGC中，∠EAB=∠GDC，AB=CD,∠EBA=∠GCD，

∴△AEB≌△DGC，

∴AE＝DG，

∴HE＝HG．

∴矩形EFGH是正方形．

解:①

在平行四边形中，

和是等腰直角三角形，

答:用含的代数式表示是

②证明:和是等腰直角三角形，

在平行四边形中，

和是等腰直角三角形，

是等腰直角三角形，

由②同理可得:

四边形是菱形，

四边形是正方形.