题目内容
在图1的扇形中，半径R=10，圆心角θ=144°，用这个扇形围成一个如图2的圆锥的侧面．
（1）求这个圆锥的底面半径r；
（2）求这个圆锥的侧面积．
解：（1）∵
，
∴
．
（2）∵r=4，l=R=10，
∴S侧=πrl=π×4×10=40π．
分析：（1）易得扇形的弧长，除以2π即为圆锥的底面半径．
（2）带圆锥的侧面积公式求解即可．
点评：考查了扇形的弧长公式，圆的周长公式；用到的知识点为：圆锥的弧长等于底面周长．
，∴
．（2）∵r=4，l=R=10，
∴S侧=πrl=π×4×10=40π．
分析：（1）易得扇形的弧长，除以2π即为圆锥的底面半径．
（2）带圆锥的侧面积公式求解即可．
点评：考查了扇形的弧长公式，圆的周长公式；用到的知识点为：圆锥的弧长等于底面周长．
练习册系列答案
相关题目
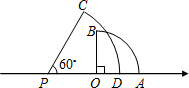以数轴上的原点O为圆心，3为半径的扇形中，圆心角∠AOB=90°，另一个扇形是以点P为圆心，5为半径，圆心角∠CPD=60°，点P在数轴上表示实数a，如图．如果两个扇形的圆弧部分（
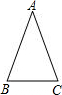如图，已知△ABC中，AB=AC，∠A=36°．