题目内容
4. 如图,已知点B、E、C、F在同一条直线上,AB=DE,∠A=∠D,AC∥DF.求证:BE=CF.
如图,已知点B、E、C、F在同一条直线上,AB=DE,∠A=∠D,AC∥DF.求证:BE=CF.
分析 欲证BE=CF,则证明两三角形全等,已经有两个条件,只要再有一个条件就可以了,而AC∥DF可以得出∠ACB=∠F,条件找到,全等可证.根据全等三角形对应边相等可得BC=EF,都减去一段EC即可得证.本题主要考查三角形全等的判定和全等三角形的对应边相等;要牢固掌握并灵活运用这些知识.
解答 证明:∵AC∥DF,
∴∠ACB=∠F,
在△ABC和△DEF中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠ACB=∠F}\\{AB=DE}\end{array}\right.$,
∴△ABC≌△DEF(AAS);
∴BC=EF,
∴BC-CE=EF-CE,
即BE=CF.
点评 本题主要考查三角形全等的判定和全等三角形的对应边相等;要牢固掌握并灵活运用这些知识.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
14.长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 9 |
12.9的算术平方根是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $\sqrt{3}$ |
2.春节前夕,咸丰县四大家在家领导与县直各单位上千名干部职工走上街头和城乡结合部的主要公路沿线,对积存的垃圾进行彻底清理,在全县掀起“洁万家”工作的热潮.学校是我家,清洁靠大家.为了让我校学生养成良好的卫生习惯,我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,统计结果如表:
根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃5个塑料袋.
(2)这天,丢弃3个塑料袋的家庭户数占总户数的40%.
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃的塑料袋有28800个.
| 每户丢弃塑料袋的个数 | 2 | 3 | 4 | 5 |
| 户 数 | 6 | 30 | 27 | 12 |
(1)这天,一个家庭一天最多丢弃5个塑料袋.
(2)这天,丢弃3个塑料袋的家庭户数占总户数的40%.
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃的塑料袋有28800个.
6.下列说法不正确的是( )
| A. | 数据3、5、4、1、-2的中位数是3 | |
| B. | 数据1、1、0、2、4的平均数是2 | |
| C. | 在选举中,人们通常最关心是数据的众数 | |
| D. | 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适 |
 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.
如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD的度数是60°.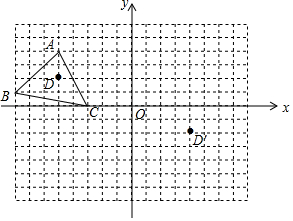 如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,
如图,把方格纸中的△ABC平移,使点D平移到点D′的位置,