Question

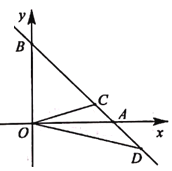
【题目】已知：∠AOB=30°，点P是∠AOB 内部及射线OB上一点，且OP=10cm．

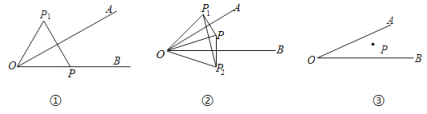
（1）若点P在射线OB上，过点P作关于直线OA的对称点，连接O、P， 如图①求P的长．

（2）若过点P分别作关于直线OA、直线OB的对称点、，连接O、O、如图②， 求的长．

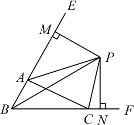
（3）若点P在∠AOB 内，分别在射线OA、射线OB找一点M，N，使△PMN的周长取最小值，请直接写出这个最小值．如图③

Answer 1

【答案】（1）= 10cm；（2）= 10cm；（3）最小值是10cm.

【解析】

（1）根据对称的性质可得OP=O，∠PO=2∠AOB=60° ，从而证出△PO是等边三角形，然后根据等边三角形的性质即可得出结论；

（2）根据对称的性质可得OP=O，OP=O ，∠PO=2∠AOP ，∠ PO=2∠BOP，然后证出△PO是等边三角形即可得出结论；

（3）过点P分别作关于直线OA、直线OB的对称点、，连接O、O、，分别交OA、OB于点M、N，连接PM、PN，根据两点之间线段最短即可得出此时△PMN的周长最小，且最小值为的长，然后根据（2）即可得出结论．

解：（1） ∵ 点P与 关于直线OA对称，∠AOB=30°

∴ OP=O，∠PO=2∠AOB=60°

∴ △PO是等边三角形

∵ OP=10cm

∴ = 10cm

（2） ∵ 点P与 关于直线OA对称，点P与关于直线OB对称，∠AOB=30°

∴ OP=O，OP=O ，∠PO=2∠AOP ，∠ PO=2∠BOP

∴ O=O，∠O=∠PO＋∠ PO=2（∠AOP＋∠BOP）=2∠AOB=60°

∴ △PO是等边三角形

∵ OP=10cm

∴ = 10cm

（3）过点P分别作关于直线OA、直线OB的对称点、，连接O、O、，分别交OA、OB于点M、N，连接PM、PN，如下图所示

根据对称的性质可得PM=M，PN=N

∴△PMN的周长=PM＋PN＋MN=M＋N＋MN=，根据两点之间线段最短可得此时△PMN的周长最小，且最小值为的长

由（2）知此时=10cm

∴△PMN的周长最小值是10cm．