��Ŀ����
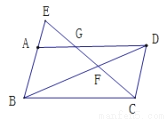
��ͼ1��ͼ2����ABC�ǵȱ������Σ�D��E�ֱ���AB��BC���ϵ��������㣨���A��B��C���غϣ���ʼ�ձ���BD=CE.
��1������D��E�˶�����ͼ1��ʾ��λ��ʱ,��֤��CD=AE.
��2����ͼ1�еġ�ACE����A��˳ʱ����ת60�㵽��ABF��λ�ã���ͼ2�����ֱ�����DF��EF.
���ҳ�ͼ�����еĵȱ�������(��ABC����)����������һ������֤����
�����ж��ı���CDFE����״,��˵������.
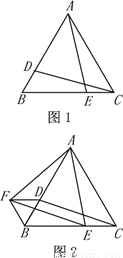
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


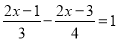 ��
��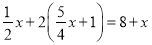 ��
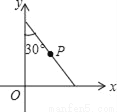
��
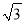 ��1�� B. ��1����
��1�� B. ��1����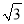 �� C. ��2
�� C. ��2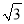 ����2�� D. ��2����2
����2�� D. ��2����2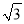 ��
�� B.
B.  C.
C.  D.
D.