Question

【题目】实践与探究

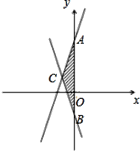
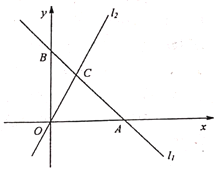
如图，在平面直角坐标系中，直线交轴于点，交轴于点，点坐标为。直线与直线相交于点，点的横坐标为1。

（1）求直线的解析式；

（2）若点是轴上一点，且的面积是面积的，求点的坐标；

Answer 1

【答案】（1）；（2）点的坐标为或

【解析】

（1）先求出C点坐标，再利用待定系数法确定函数关系式即可求解；

（2）先求出A点坐标，再过点作轴，垂足为点；过点作轴，垂足为点，设点的坐标为，根据三角形的面积即可列出式子求解；

解：（1）∵点在上，且横坐标是1，

∴把代入中，得，

∴点的坐标为，

设直线的解析式为，将点的坐标代入得

解得

∴直线的解析式为；

（2）∵点是直线与轴的交点，

∴把代入中得，，∴点坐标为，

过点作轴，垂足为点；过点作轴，垂足为点，

由点的坐标为可得，，

设点的坐标为，

依题意得，，

即，

解得，，

∴点的坐标为或；