题目内容
如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°.

(1)求证:CA=CD;
(2)求证:BD=OB.
【答案】
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据切线的性质,推出∠A,∠D的度数,即可推出结论;
(2)根据含30度角的直角三角形的性质即可推出结论.
试题解析:(1)∵CD切⊙O于点C,∴∠OCD=90°.
∵∠ACD=120°,∴∠ACO=30°.
∵AB是⊙O的直径,∴OA=OC=OB. ∴∠A=30°. ∴∠D=30°. ∴CA=CD.
(2)∵Rt△ODC中,∠D=30°,∴OC= OD.
OD.
又∵OC=OB,∴OB= OD,即BD=OB.
OD,即BD=OB.
考点:1. 切线的性质;2.等腰三角形的性质;3. 含30度角的直角三角形的性质.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
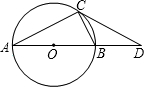 如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).
如图,已知:AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和所给图形,写出8个正确的结论(除AO=OB=BD外).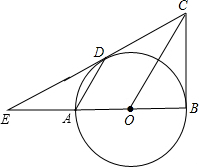 CD的延长线的交点.
CD的延长线的交点.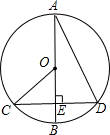 如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.
如图,已知:AB是⊙O的直径,CD⊥AB于E,连接AD、OC.

 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是