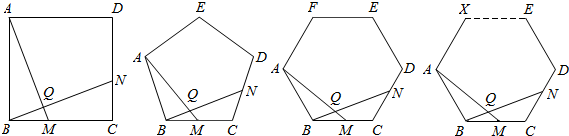
题目内容
已知正六边形ABCDEF的边长为1,QR是正六边形内平行于AB的任意线段,求以QR为底边的内接于正六边形ABCDEF的△PQR的最大面积.分析:要使△PQR的面积最大,P点应在DE上;Q,R点应分别在AF、BC上.过P点PH⊥QR于H,交AB于G,过A,B分别作AM⊥QR于M,BN⊥QR于.可设PH=x,再用含x的式子表示QR,根据平方的非负性,得出△PQR的最大面积.
解答: 解:过P点PH⊥QR于H,交AB于G,过A,B分别作AM⊥QR于M,BN⊥QR于N.
解:过P点PH⊥QR于H,交AB于G,过A,B分别作AM⊥QR于M,BN⊥QR于N.
设PH=x,则HG=
-x.
QM=NR=AM•tan30°=1-
x,
QR=2(1-
x)+1=3-
x,
△PQR的面积=
(3-
x)x=-
(x-
)2+
,
当x=
,即当Q,R分别在AF、BC的中点时,△PQR的最大面积为
.
 解:过P点PH⊥QR于H,交AB于G,过A,B分别作AM⊥QR于M,BN⊥QR于N.
解:过P点PH⊥QR于H,交AB于G,过A,B分别作AM⊥QR于M,BN⊥QR于N.设PH=x,则HG=
| 3 |
QM=NR=AM•tan30°=1-
| ||
| 3 |
QR=2(1-
| ||
| 3 |
| 2 |
| 3 |
| 3 |
△PQR的面积=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
3
| ||
| 4 |
9
| ||
| 16 |
当x=
3
| ||
| 4 |
9
| ||
| 16 |
点评:本题综合性较强,考查了三角形的面积,平方的非负性,三角函数等知识,有一定的难度.

练习册系列答案
相关题目



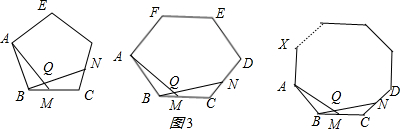
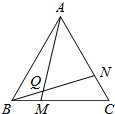 (1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,∠BAM=∠NBC,猜想∠BQM等于多少度,并证明你的猜想.
(1)已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,∠BAM=∠NBC,猜想∠BQM等于多少度,并证明你的猜想.