Question

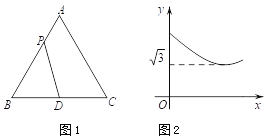
【题目】如图1，在等边△ABC中，点D是BC边的中点，点P为AB边上的一个动点，设，图1中线段DP的长为，若表示与的函数关系的图象如图2所示，则等边△ABC的面积为_____.

Answer 1

【答案】4.

【解析】

从图2的函数图象为抛物线得知，y与x满足二次函数关系，同时y的最小值为，结合等边三角形的图形可知，当点P运动到DP⊥AD位置时，DP长为最小值，利用等边三角形的特殊角可求出边长，从而得出等边三角形△ABC的面积．

解：由图二可得y最小值=，

∵△ABC为等边三角形，分析图一可知，当P点运动到DP⊥AB时，DP长为最小值，

∴此时的DP=，

∵∠B=60°，

∴sin60°=，

解得BD=2，

∵D为BC的中点，

∴BC=4，连接AD，

∵△ABC为等边三角形，

∴AD⊥BC，

，

，

.