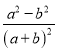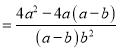Question

【题目】我们定义：两个二次项系数之和为1，对称轴相同，且图象与y轴交点也相同的二次函数互为友好同轴二次函数例如：的友好同轴二次函数为．

请你分别写出，的友好同轴二次函数；

满足什么条件的二次函数没有友好同轴二次函数？满足什么条件的二次函数的友好同轴二次函数是它本身？

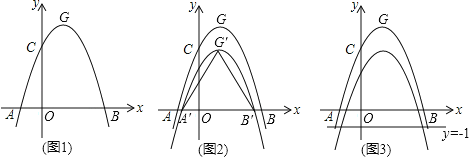
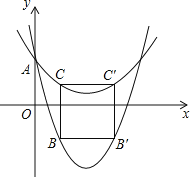
如图，二次函数：与其友好同轴二次函数都与y轴交于点A，点B、C分别在、上，点B，C的横坐标均为，它们关于的对称轴的对称点分别为，，连结，，，CB．

若，且四边形为正方形，求m的值；

若，且四边形的邻边之比为1：2，直接写出a的值．

Answer 1

【答案】函数的友好同轴二次函数为；函数的友好同轴二次函数为；二次项系数为1的二次函数没有友好同轴二次函数；二次项系数为的二次函数的友好同轴二次函数是它本身；的值为；的值为、、或．

【解析】

(1)根据友好同轴二次函数的定义，找出、的友好同轴二次函数即可；

(2)由二次项系数非零可得出二次项系数为1的二次函数没有友好同轴二次函数，由友好同轴二次函数的定义可知：二次项系数为的二次函数的友好同轴二次函数是它本身；

(3)根据二次函数L_1的解析式找出其友好同轴二次函数L_2的函数解析式．

①代入a=3，利用二次函数图象上点的坐标特征可得出点B、C、B'、C'的坐标，进而可得出BC、BB'的值，由正方形的性质可得出BC=BB'，即关于m的一元二次方程，解之取其大于0小于2的值即可得出结论；

②由m=1，利用二次函数图象上点的坐标特征可得出点B、C、B'、C'的坐标，进而可得出BC、BB'的值，由两边之比为1：2，即可得出关于a的含绝对值符号的一元一次方程，解之即可得出结论．

，

函数的友好同轴二次函数为；

，，

函数的友好同轴二次函数为．

，

二次项系数为1的二次函数没有友好同轴二次函数；

，

二次项系数为的二次函数的友好同轴二次函数是它本身．

二次函数：的对称轴为直线，其友好同轴二次函数：．

，

二次函数：，二次函数：，

点B的坐标为，点C的坐标为，

点的坐标为，点的坐标为，

，．

四边形为正方形，

，即，

解得：，不合题意，舍去，

的值为．

当时，点B的坐标为，点C的坐标为，

点的坐标为，点的坐标为，

，．

四边形的邻边之比为1：2，

或，即或，

解得：，，，，

的值为、、或．