题目内容
(本题满分12分)已知:关于x的一元二次方程
(1)求证:方程有两个实数根;
(2)设m<0,且方程的两个实数根分别为 ,
, (其中
(其中 <
< ),若y是关于m的函数,且
),若y是关于m的函数,且 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,利用函数图象求关于m的方程 的解。
的解。

(1)详见解析;(2) (m<0);(3)当m<0时,方程
(m<0);(3)当m<0时,方程 的解为m=-1
的解为m=-1
【解析】
试题分析:(1)证明:∵  是关于x的一元二次方程,
是关于x的一元二次方程,

∵ m2?0,
∴ 原方程有实数根.
(2)解:由求根公式,得

∴ x=m+1或 .
.
∵ m<0,∴ m+1<1.
∵  <
< ,∴ x1=m+1, x2= 1.
,∴ x1=m+1, x2= 1.
∴  .即
.即 (m<0)为所求.
(m<0)为所求.
(3)解法一:如图1, 在同一平面直角坐标系中分别画出 (m<0)
(m<0)
与y=-m+3(m<0)的图象.
由图象可得当m<0时,方程 的解为m=-1.
的解为m=-1.
解法二:如图2, 在同一平面直角坐标系中分别画出 (m<0)
(m<0)
与y=m-3(m<0)的图象.
由图象可得当m<0时,方程 的解为m=-1.
的解为m=-1.

图1 图2
考点:1.跟与系数的关系;2.函数图象的交点

练习册系列答案
相关题目
 ,y1),B(2,y2),C(﹣
,y1),B(2,y2),C(﹣ ,y3)则
,y3)则 的大小关系为( )
的大小关系为( )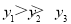 B.
B. C.
C. D.
D.
 ,0.5,
,0.5,  ,其中为无理数的是( )
,其中为无理数的是( ) C.0.5 D.
C.0.5 D.
 的图像如图所示,若
的图像如图所示,若 有两个不相等的实数根, 则k 的取值范围是( )
有两个不相等的实数根, 则k 的取值范围是( )
 B.
B. C.
C. D.
D.
 绕着原点旋转180°,所得抛物线的解析式是( )
绕着原点旋转180°,所得抛物线的解析式是( ) B.
B.
 D.
D.
 中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在
中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在 轴的负半轴和
轴的负半轴和 轴的正半轴上,抛物线
轴的正半轴上,抛物线 经过点A、B,且18
经过点A、B,且18 +
+ =0.
=0.
 是
是 的平方根;⑤两个无理数的和一定是无理数或零,其中正确的说法有( )
的平方根;⑤两个无理数的和一定是无理数或零,其中正确的说法有( )