题目内容
解:∠A+∠B+∠C=180°
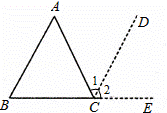
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD ( )
∴∠B= ∠2 ( )
而∠ACB+∠1+∠2=180°
∴∠ACB+ ∠B + ∠A =180°( )
考点:三角形内角和定理。
专题:推理填空题。
分析:作∠ACD=∠A,并延长BC到E.利用平行线的判定推知AB∥CD,然后根据平行线的性质可知∠B=∠2;最后由等量代换证得∠ACB+∠B+∠A=180°.
解答:解:∠A+∠B+∠C=180°.
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD (内错角相等,两直线平行 )
∴∠B=∠2(两直线平行,同位角相等 )
而∠ACB+∠1+∠2=180°
∴∠ACB+∠B+∠A=180°(等量代换).
故答案是:内错角相等,两直线平行;∠2;两直线平行,同位角相等;∠B;∠A.

点评:本题考查了三角形内角和定理.在证明三角形内角和定理时,充分利用了平行线的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
是方程x+5ky=5k的一个解,则k的值是( )
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
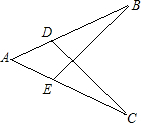 如图:已知∠B=∠C,AD=AE,则AB=AC,请说明理由(填空)
如图:已知∠B=∠C,AD=AE,则AB=AC,请说明理由(填空)