题目内容
 如图,CD是⊙O的直径,AB是弦,且AB⊥CD,E为垂足,则下列结论中正确的有
如图,CD是⊙O的直径,AB是弦,且AB⊥CD,E为垂足,则下列结论中正确的有
(1)AE=BE;(2)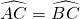 ;(3)
;(3) ;(4)OE=DE.
;(4)OE=DE.
- A.4个
- B.3个
- C.2个
- D.1个
B
分析:由CD是⊙O的直径,AB是弦,且AB⊥CD,E为垂足,根据垂径定理即可得(1)AE=BE;(2)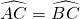 ;(3)
;(3) ;继而求得答案.
;继而求得答案.
解答:∵CD是⊙O的直径,AB⊥CD,
∴AE=BE,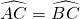 ,
, ,
,
故(1),(2),(3)正确;
∵E不一定是OD的中点,
即OE不一定等于DE,
故(4)错误.
∴正确的有3个.
故选B.
点评:此题考查了垂径定理.此题难度不大,注意掌握垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
分析:由CD是⊙O的直径,AB是弦,且AB⊥CD,E为垂足,根据垂径定理即可得(1)AE=BE;(2)
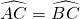 ;(3)
;(3) ;继而求得答案.
;继而求得答案.解答:∵CD是⊙O的直径,AB⊥CD,
∴AE=BE,
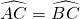 ,
, ,
,故(1),(2),(3)正确;
∵E不一定是OD的中点,
即OE不一定等于DE,
故(4)错误.
∴正确的有3个.
故选B.
点评:此题考查了垂径定理.此题难度不大,注意掌握垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目


 (2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(
(2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高( 如图,某水库堤坝的横断面为梯形,背水坡AD的坡比(坡比是斜坡的铅直距离与水平距离的比)为1:1.5,迎水坡BC的坡比为1:
如图,某水库堤坝的横断面为梯形,背水坡AD的坡比(坡比是斜坡的铅直距离与水平距离的比)为1:1.5,迎水坡BC的坡比为1: