Question

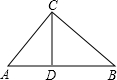如图在△ABC中，CD是边AB上的高，AC=3，BC=4，AB=5，则CD的长是

 

．

Answer 1

考点：勾股定理的逆定理,三角形的面积

专题：

分析：由题干条件知：AC²+BC²=AB²，根据勾股定理的逆定理可知三角形为直角三角形，根据三角形的面积相等即可求出CD的长．

解答：解：在△ABC中，∵AC=3，BC=4，AB=5，
∴AC²+BC²=AB²，
∴△ABC是直角三角形，且∠ACB=90°．
根据三角形面积相等可知，

1

2

BC•AC=

1

2

AB•CD，
∴CD=

BC•AC

AB

=

4×3

5

=2.4，
故答案为2.4．

点评：本题主要考查勾股定理的逆定理的知识点，此题难度一般，利用好勾股定理的逆定理是解答本题的关键．