题目内容
在△ABC中,∠A,∠B均为锐角,且sinA=
,cosB=
,AC=40,则△ABC的面积是( )
| 1 |
| 2 |
| ||
| 2 |
| A、800 | ||
B、800
| ||
| C、400 | ||
D、400
|
考点:解直角三角形
专题:计算题
分析:如图所示,过C作CD⊥AB,根据题意,利用锐角三角函数定义求出∠A与∠B的度数,利用等角对等边得到AC=BC,利用三线合一得到D为AB中点,在直角三角形ACD中,利用30度所对的直角边等于斜边的一半求出CD的长,利用勾股定理求出AD的长,确定出AB的长,求出三角形ABC面积即可.
解答: 解:如图所示,过C作CD⊥AB,
解:如图所示,过C作CD⊥AB,
∵在△ABC中,∠A,∠B均为锐角,且sinA=
,cosB=
,
∴∠A=∠B=30°,
∴BC=AC,
∴D为AB中点,
在Rt△ACD中,AC=40,
∴CD=
AC=20,
根据勾股定理得:AD=
=20
,
∴AB=2AD=40
,
则△ABC的面积是
AB•CD=400
,
故选D
 解:如图所示,过C作CD⊥AB,
解:如图所示,过C作CD⊥AB,∵在△ABC中,∠A,∠B均为锐角,且sinA=
| 1 |
| 2 |
| ||
| 2 |
∴∠A=∠B=30°,
∴BC=AC,
∴D为AB中点,
在Rt△ACD中,AC=40,
∴CD=
| 1 |
| 2 |
根据勾股定理得:AD=
| AC2-CD2 |
| 3 |
∴AB=2AD=40
| 3 |
则△ABC的面积是
| 1 |
| 2 |
| 3 |
故选D
点评:此题属于解直角三角形,涉及的知识有:锐角三角函数定义,勾股定理,以及三角形面积求法,熟练掌握直角三角形的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=70°,则∠3=( )
如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=70°,则∠3=( )| A、50° | B、60° |
| C、70° | D、80° |
下列运算中,正确的是( )
| A、(a+b)2=a2+b2 |
| B、a+a=a2 |
| C、(a2)3=a6 |
| D、5a-2a=3 |
根据下列已知条件,能唯一画出△ABC的是( )
| A、AB=5,BC=3,AC=8 |
| B、AB=4,BC=3,∠A=30° |
| C、∠C=90°,AB=6 |
| D、∠A=60°,∠B=45°,AB=4 |
 已知:如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.
已知:如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒. 如图,若∠BAC=∠1,则
如图,若∠BAC=∠1,则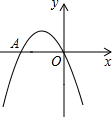 如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).
如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).