Question

12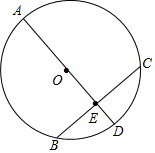．如图，已知AD是⊙O的直径，BC是⊙O的弦，AD⊥BC，垂足为点E，AE=BC=16，求⊙O的直径．

Answer 1

分析 连接OB，根据垂径定理求出BE，根据勾股定理得出方程，求出方程的解即可．

解答 解：
连接OB，设OB=OA=R，则OE=16-R，
∵AD⊥BC，BC=16，
∴∠OEB=90°，BE=$\frac{1}{2}$BC=8，
由勾股定理得：OB²=OE²+BE²，
R²=（16-R）²+8²，
解得：R=10，
即⊙O的直径为20．

点评 本题考查了垂径定理，勾股定理的应用，能根据垂径定理求出BE的长是解此题的关键，注意：垂直于弦的直径平分弦．