题目内容
3.学校为了改善办学条件,需要购买500套桌椅,已知甲种桌椅每套150元,乙种桌椅每套120元.(1)若总共花费66000元,则购买甲、乙两种桌椅各多少套?
(2)若购买甲种桌椅的费用不少于购买乙种桌椅费用,则要选择怎样购买方案才能使费用最少?最少费用是多少?
分析 (1)设购买甲种桌椅x套,则购买乙种桌椅(500-x)套,根据购买费用=单价×数量可列出关于x的一元一次方程,解方程即可得出结论;
(2)根据甲种桌椅的费用不少于购买乙种桌椅费用列出关于x的一元一次不等式,解不等式得出x的值域,根据购买费用=单价×数量可得出总费用w关于x的一次函数,根据函数的单调性即可得出结论.
解答 解:(1)设购买甲种桌椅x套,则购买乙种桌椅(500-x)套,
根据题意得:150x+120(500-x)=66000,
解得:x=200,
500-200=300(套).
答:购买甲种桌椅200套,则购买乙种桌椅300套.
(2)设购买甲种桌椅x套,则购买乙种桌椅(500-x)套,
根据题意得:150x≥120(500-x),
解得:x≥$\frac{2000}{9}$=222$\frac{2}{9}$.
购买桌椅费用w=150x+120(500-x)=30x+60000,
当正整数x最小时,费用最少.
所以当购买甲种桌椅223套,乙种桌椅277套时费用最少,最少费用为30×223+60000=66690(元).
点评 本题考查了一元一次不等式的应用、一元一次方程的应用以及一次函数的性质,解题的关键:(1)列出关于x的一元一次方程;(2)找出w关于x的函数关系式并通过解一元一次不等式得出x的取值范围.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.

练习册系列答案
相关题目
13.已知A(1,1)、B(3,2),点B绕点A逆时针旋转90°到达点C处,则点C的坐标是( )
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
11.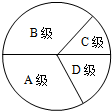 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
根据以上提供的信息解答下列问题:
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
 为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:| 等级 | A级(优秀) (≥108分) | B级(良好) (≥84分且<108分) | C级(及格) (≥72分且<84分) | D级(不及格) (<72分) |
| 人数 | 22 | 28 | 18 |
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.
8.与$\sqrt{5}$最接近的整数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
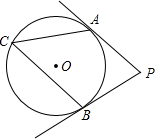 如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.
如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.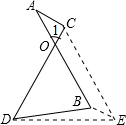 如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因.
如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因.