题目内容
设等式 +
+ =
= -
- 在实数范围内成立,其中a、x、y是两两不同的实数,求
在实数范围内成立,其中a、x、y是两两不同的实数,求 的值.
的值.
【答案】分析:已知等式右边成立,x-a≥0,a-y≥0,即y-a≤0;由等式左边成立可知,a=0,已知等式可变为 -
- =0,移项、开平方得x=-y,利用代入法求式子的值.
=0,移项、开平方得x=-y,利用代入法求式子的值.
解答:解:∵ +
+ =
= -
- 在实数范围内成立,
在实数范围内成立,
∴x-a≥0,a-y≥0,即y-a≤0,
代入左边可知,a=0,
原等式可变为 -
- =0,解得x=-y,
=0,解得x=-y,
∴ =
= =
= .
.
点评:本题考查了二次根式的意义的运用,关键是通过分析左右两边四个二次根式有意义,得出a的值.
 -
- =0,移项、开平方得x=-y,利用代入法求式子的值.
=0,移项、开平方得x=-y,利用代入法求式子的值.解答:解:∵
 +
+ =
= -
- 在实数范围内成立,
在实数范围内成立,∴x-a≥0,a-y≥0,即y-a≤0,
代入左边可知,a=0,
原等式可变为
 -
- =0,解得x=-y,
=0,解得x=-y,∴
 =
= =
= .
.点评:本题考查了二次根式的意义的运用,关键是通过分析左右两边四个二次根式有意义,得出a的值.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 在实数范围内成立,其中a、x、y是两两不同的实数,则
在实数范围内成立,其中a、x、y是两两不同的实数,则 =________
=________ +
+ =
=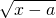 -
- 在实数范围内成立,其中a、x、y是两两不同的实数,求
在实数范围内成立,其中a、x、y是两两不同的实数,求 的值.
的值. +
+ =
= +
+ 在实数范围内成立,其中a,x,y实数,则
在实数范围内成立,其中a,x,y实数,则 的值为 .
的值为 . 在实数范围内成立,其中a、x、y是两两不同的实数,则
在实数范围内成立,其中a、x、y是两两不同的实数,则 的值是( )
的值是( )
