题目内容
20. 在正方形ABCD中,M、N分别是边CD、AD的中点,连接BN,AM交于点E.求证:AM⊥BN.
在正方形ABCD中,M、N分别是边CD、AD的中点,连接BN,AM交于点E.求证:AM⊥BN.
分析 先根据SAS证明△ABN≌△DAM,得出对应角相等∠ABN=∠DAM,再根据角的互余关系即可得出∠AEB=90°,证出AM⊥BN.
解答 证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAN=∠ADM=90°,
∵M、N分别是边CD、AD的中点,
∴AN=$\frac{1}{2}$AD,DM=$\frac{1}{2}$CD,
∴AN=DM,
在△ABN和△DAM中,$\left\{\begin{array}{l}{AB=DA}&{\;}\\{∠BAN=∠ADM}&{\;}\\{AN=DM}&{\;}\end{array}\right.$,
∴△ABN≌△DAM(SAS),
∴∠ABN=∠DAM,
∵∠DAM+∠BAE=90°,
∴∠ABN+∠BAE=90°,
∴∠AEB=90°,
∴AM⊥BN.
点评 本题考查了正方形的性质以及全等三角形的判定与性质;证明三角形全等得出角相等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
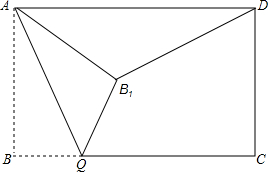 如图,长方形ABCD中AB=2,BC=4,点Q是线段BC上一点,连接AQ,作点B关于直线AQ的对称点B,连接AB1,QB1.
如图,长方形ABCD中AB=2,BC=4,点Q是线段BC上一点,连接AQ,作点B关于直线AQ的对称点B,连接AB1,QB1. 如图,已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么?
如图,已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么? 如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).