题目内容
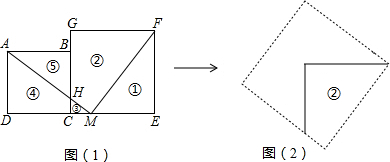
(2012•龙岩质检)如图(1)是由边长为3和4的两个正方形拼成的图形,将将该图剪成如图所示序号分别为①②③④⑤的五部分,再将它拼成一个大正方形.
(1)大正方形的边长为
(2)请在图(2)完成拼图(画出,并在图上标出相应序号);
(3)求图(1)中线段BH的长度.
(1)大正方形的边长为
5
5
;(2)请在图(2)完成拼图(画出,并在图上标出相应序号);
(3)求图(1)中线段BH的长度.

分析:(1)根据拼接后的正方形的面积等于拼接前两个正方形的面积的和列式计算即可得解;
(2)根据正方形的边长相等可得①在②的上边,③、④逆时针旋转90°使AD到AB的位置;
(3)根据勾股定理列式求出ME,再求出CM,然后利用△ABH和△MCH相似,根据相似三角形对应边成比例列式计算即可得解.
(2)根据正方形的边长相等可得①在②的上边,③、④逆时针旋转90°使AD到AB的位置;
(3)根据勾股定理列式求出ME,再求出CM,然后利用△ABH和△MCH相似,根据相似三角形对应边成比例列式计算即可得解.
解答: 解:(1)拼接的大正方形的面积=32+42=25,
解:(1)拼接的大正方形的面积=32+42=25,
所以,大正方形的边长=5;
故答案为:5;
(2)拼图如图所示;
(3)如图(1),由(1)有:MF=5,FE=4,
根据勾股定理,ME=
=
=3,
∴CM=1,
设BH=x,则CH=3-x,
∵AB∥CM,
∴△ABH∽△MCH,
∴
=
,
即
=
,
解得x=
,
即BH=
.
 解:(1)拼接的大正方形的面积=32+42=25,
解:(1)拼接的大正方形的面积=32+42=25,所以,大正方形的边长=5;
故答案为:5;
(2)拼图如图所示;
(3)如图(1),由(1)有:MF=5,FE=4,
根据勾股定理,ME=
| MF2-FE2 |
| 52-42 |
∴CM=1,
设BH=x,则CH=3-x,
∵AB∥CM,
∴△ABH∽△MCH,
∴
| AB |
| CM |
| BH |
| HC |
即
| 3 |
| 1 |
| x |
| 3-x |
解得x=
| 9 |
| 4 |
即BH=
| 9 |
| 4 |
点评:本题考查了图形的拼接,主要利用了正方形的性质,根据正方形的边长相等是确定拼接部分的位置的关键,还利用了勾股定理以及相似三角形的判定与性质.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
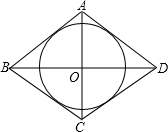 (2012•龙岩质检)如图,菱形ABCD中,若AC=6,BD=8,则该菱形的内切圆半径r=
(2012•龙岩质检)如图,菱形ABCD中,若AC=6,BD=8,则该菱形的内切圆半径r=