题目内容
 如图,已知等腰梯形ABCD的腰AB=CD=m,对角线AC⊥BD,锐角∠ABC=α,则该梯形的面积是
如图,已知等腰梯形ABCD的腰AB=CD=m,对角线AC⊥BD,锐角∠ABC=α,则该梯形的面积是
- A.2msinα
- B.m2(sinα)2
- C.2mcosα
- D.m2(cosα)2
B
分析:在等腰梯形ABCD中,对角线AC⊥BD,所以,AC=BD,则,∠ACB=45°;利用正弦定理得, ,可得出AC的值,所以,S等腰梯形ABCD=
,可得出AC的值,所以,S等腰梯形ABCD= ×AC×BD,代入数值,解答出即可.
×AC×BD,代入数值,解答出即可.
解答:在等腰梯形ABCD中,对角线AC⊥BD,
∴AC=BD,则,∠ACB=45°,
又∠ABC=α,AB=CD=m,
∴由正弦定理得, ,
,
∴AC=msinα÷sin45°,
= msinα,
msinα,
∴S等腰梯形ABCD= ×AC×BD,
×AC×BD,
= ×
× msinα×
msinα× msinα,
msinα,
=m2(sinα)2.
故选B.
点评:本题考查了直角三角形、等腰梯形的性质,注意题目中的隐含条件,∠ACB=∠DBC=45°,是解答本题的关键.
分析:在等腰梯形ABCD中,对角线AC⊥BD,所以,AC=BD,则,∠ACB=45°;利用正弦定理得,
 ,可得出AC的值,所以,S等腰梯形ABCD=
,可得出AC的值,所以,S等腰梯形ABCD= ×AC×BD,代入数值,解答出即可.
×AC×BD,代入数值,解答出即可.解答:在等腰梯形ABCD中,对角线AC⊥BD,
∴AC=BD,则,∠ACB=45°,
又∠ABC=α,AB=CD=m,
∴由正弦定理得,
 ,
,∴AC=msinα÷sin45°,
=
 msinα,
msinα,∴S等腰梯形ABCD=
 ×AC×BD,
×AC×BD,=
 ×
× msinα×
msinα× msinα,
msinα,=m2(sinα)2.
故选B.
点评:本题考查了直角三角形、等腰梯形的性质,注意题目中的隐含条件,∠ACB=∠DBC=45°,是解答本题的关键.

练习册系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为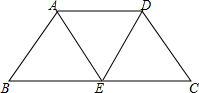 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是