��Ŀ����
����Ŀ�����Ƕ���:���һ��������һ�����ϵĸߵ���������,��ô��������ν������ȸߵ���������,�����߽�����������ε����ȵ�����
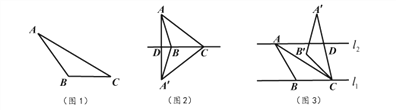
��1����������:
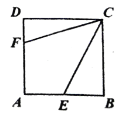
��ͼ1,��![]() ��,
��,![]() ,
,![]() .
.![]() ,���ж�
,���ж�![]() �Ƿ������ȸߵ��������Σ���˵������.
�Ƿ������ȸߵ��������Σ���˵������.
��2������̽��:
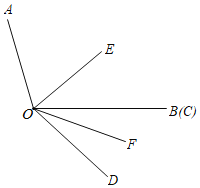
��ͼ2, ![]() �����ȸߵ���������,
�����ȸߵ���������,![]() �����ȵ�������
�����ȵ�������![]() ����
����![]() ����ֱ�ߵĶԳ�ͼ�εõ�
����ֱ�ߵĶԳ�ͼ�εõ�![]() ,����
,����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() .����
.����![]() ��
��![]() ������,��
������,��![]() ��ֵ.
��ֵ.
��3��Ӧ����չ:
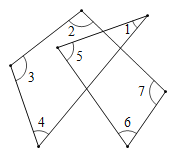
��ͼ3,��֪![]() ,
,![]() ��
��![]() ֮��ľ���Ϊ2.���ȸߵ���
֮��ľ���Ϊ2.���ȸߵ���![]() �����ȵ���
�����ȵ��� ![]() ��ֱ��
��ֱ��![]() ��,��
��,��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��.��
��.��![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() �õ�
�õ�![]() ,
,![]() ����ֱ�߽�
����ֱ�߽�![]() �ڵ�
�ڵ�![]() .��
.��![]() ��ֵ.
��ֵ.
���𰸡���1��֤������������2��![]() ��3��
��3��![]() ��ֵΪ
��ֵΪ![]() ,
,![]() ,2
,2
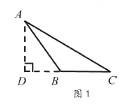
����������1������A��AD��ֱ��CB�ڵ�D�����Եõ�AD=BC=3�����ɵõ����ۣ�
��2������ ��ABC�ǡ��ȸߵס������Σ�BC�ǡ��ȵס����õ�AD=BC�� ���� ��A��BC�릤ABC����ֱ��BC�Գƣ� �õ� ��ADC=90�㣬�����ĵ����ʣ��õ�BC=2BD����BD=x����AD=BC=2x�� CD=3x ���ɹ��ɶ�����AC=![]() x�����ɵõ����ۣ�
x�����ɵõ����ۣ�
��3��������������ۼ������ٵ�AB=![]() BCʱ���ٷ�����������ۣ�
BCʱ���ٷ�����������ۣ�
�ڵ�AC=![]() BCʱ���ٷ�����������ۼ��ɣ�
BCʱ���ٷ�����������ۼ��ɣ�
��1���ǣ��������£�
��ͼ1������A��AD��ֱ��CB�ڵ�D��
�তADCΪֱ�������Σ���ADC=90�㣮
�� ��ACB=30�㣬AC=6���� AD=![]() AC=3��
AC=3��
�� AD=BC=3��
����ABC�ǡ��ȸߵס������Σ�
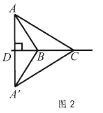
��2����ͼ2�� �� ��ABC�ǡ��ȸߵס������Σ�BC�ǡ��ȵס�����AD=BC��
�� ��A��BC�릤ABC����ֱ��BC�Գƣ� �� ��ADC=90�㣮
�ߵ�B�Ǧ�AA��C�����ģ� �� BC=2BD��
��BD=x����AD=BC=2x����CD=3x ��
���ɹ��ɶ�����AC=![]() x��
x��
��![]() ��
��
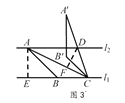
��3���ٵ�AB=![]() BCʱ��
BCʱ��
������ͼ3����AE��l1�ڵ�E�� DF��AC�ڵ�F��
�����ȸߵ��� ��ABC�����ȵ���ΪBC��l1//l2��
l1��l2֮��ľ���Ϊ2�� AB=![]() BC��
BC��
��BC=AE=2��AB=2![]() ��
��
��BE=2����EC=4����AC= ![]() ��
��
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A' B' C�����CDF=45�㣮
��DF=CF=x ��
��l1//l2�����ACE=��DAF����![]() ����AF=2x��
����AF=2x��
��AC=3x=![]() ���ɵ�x=
���ɵ�x=![]() ����CD=
����CD=![]() x=
x=![]() ��
��
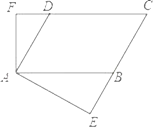
������ͼ4����ʱ��ABC�ǵ���ֱ�������Σ�
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A' B' C��
�� ��ACD�ǵ���ֱ�������Σ�
�� CD=![]() AC=
AC=![]() ��
��
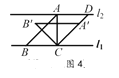
�ڵ�AC=![]() BCʱ��
BCʱ��
������ͼ5����ʱ��ABC�ǵ���ֱ�������Σ�
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45��õ���A�� B��C��
��A��C��l1����CD=AB=BC=2��
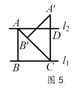
������ͼ6����AE��l1�ڵ�E����AE=BC��
��AC=![]() BC=
BC=![]() AE�����ACE=45�㣬
AE�����ACE=45�㣬
�তABC�Ƶ�C��˳ʱ�뷽����ת45��õ���A�� B��Cʱ��
��A����ֱ��l1�ϣ�
��A��C��l2����ֱ��A�� C��l2���㣮
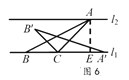
����������CD��ֵΪ![]() ��
��![]() ��2��
��2��